ブログ
学習コラム
【高校受験】解けないとヤバい数学の入試本番レベルの問題を解説付きでご紹介
2024.05.02
【分野別】解けないとヤバい数学の本番レベルの問題を解説付きでご紹介
実際の入試本番レベルの「解けないとヤバい」数学の問題を分野別にピックアップしていますので、実際に手を動かして解いてみましょう。解答解説もつけていますので、答えの正誤に加えて、「考え方」が合っているのかまで丁寧に確認するのがオススメです。
解けないとヤバい平面図形の問題と解説
はじめは平面図形に関する必須の問題です。今回は「合同・相似の証明」から問題をピックアップしています。この分野は、条件を覚えたり、証明を組み立てたりと、高校受験数学の中ではやることが多いですが、その分、入試問題はセオリー通りであることがほとんどです。今回ご紹介する問題の他にも、参考書などで証明のパターンを覚えてしまうまで練習しましょう。
問題『三角形と相似』に関する問題
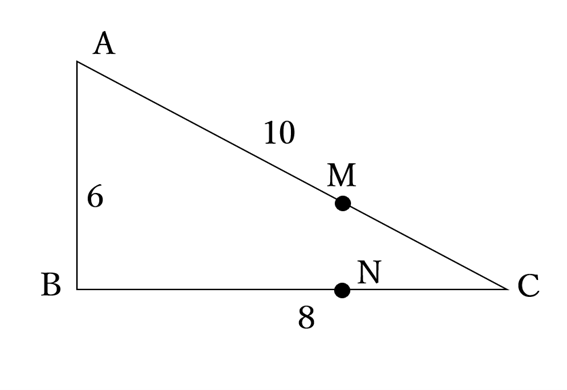
上の図のように、次のような条件が与えられる三角形ABC について。AB=6、BC=8、AC=10とする。M をAC 上の点で、AM:MC=2:1 を満たすものとし、N をBC 上の点で、BN:NC=2:1を満たすものとする。
このとき、△MNC は△ABC と相似であることを証明せよ。
解答・解説
解答)
AM:MC=2:1, BN:NC=2:1より辺MNと辺ABは平行であることは明らかである。これより、
∠ABC=∠MNC=90°・・・①
また、共通角として、
∠ACB=∠MCN・・・②
①と②より、2組の角がそれぞれ等しいので△MNC と△ABC は相似である。
解説)
今回の問題は、相似の証明の中ではかなり標準的です。証明に用いた、条件としては「2組の角がそれぞれ等しい」で、この条件が答えになる入試問題は頻出傾向にあります。
また、この問題は別解として、AM:MC=2:1, BN:NC=2:1を用いて、実際にすべての三角形の辺を求めることができるため、「3組の辺の比がすべて等しい」相似条件を使うこともできます。
入試問題の難易度が上がるにつれ、使える条件が絞られ、相似な三角形を探すのが難しくなってきます。
解けないとヤバい空間図形の問題と解説
続いては空間図形に関する問題です。一問一答形式の図形の公式を使った問題は解ける学生でも、空間図形になると途端に解けなくなることはよくあります。
まずは以下の問題にチャレンジしてみましょう。
(ヒント:中学校の図形の公式で最も簡単な公式を使います)
問題『点と直線』に関する問題
1辺の長さが6cm の立方体ABCD-EFGHがあり、辺ADの中点をM、辺FGの中点をNとする。また、EH上にはEP=3cmとなるように点Pが存在する。このときMNの長さを求めなさい。
解答解説
解答)
FN上の点Nは、FGの中点なので、FN=3。
また、この立体は立方体であることから、四角形EFGHのすべての角が90°。
四角形EFNPについて考えてみると、EP=FN=3,かつEFとNPは平行より、
NP=6cm・・・①
同様に四角形AEPMに関しても考えると、
PM=6cm・・・②
次に△MNPに関して考えると、辺MPは辺AD,DHと並行であることから、
∠MPN=90° とわかる。
よって直角三角形であることから、三平方の定理を使って、
MN2NP2+MP2=62+62=√72 有利化すると MN=6√2
解説)
最重要ポイントとして、空間図形は必ず作図してから解答を考えてください。
この問題で使った数学の公式は「三平方の定理」のみ。ただし、公式を使うまでに「図形に注目したらよいか?」に気づけないと答えを導き出せません。
このような空間図形の問題は、「答えとして何を導き出せばよいか確認」→「その答えは平面図形としては何か考える」→「空間図形のどこを切り取るか探す」の順で逆にたどるのがコツです。
例えばこの問題なら、「MNを求めたい」→「直角三角形の斜辺である」→「立方体を中点で分断している三角形がある」といった感じです。
解けないとヤバい方程式・関数の問題と解説
続いては関数や方程式に関する問題です。ここでは、最も基本的である一次関数を利用した入試レベルの問題に挑戦してもらいます。関数の分野は問題が多種多用であるため、パターンを覚えるのではなく、「どうやったら関数の問題になるか?」変換するトレーニングが合格のカギになります。
問題『一次関数』に関する問題
A君はAM9:00家から20km先の駅に自転車で向かい、家を出発して2時間後に駅に到着しました。駅から時速100㎞の電車に乗って、12:00に学校に到着しました。以下の問に答えなさい。
(1)A君は平均時速何キロで駅に向かいましたか。
(2)A君の家から学校までは何キロですか。
解答)
(1)について
時間をx,移動距離(km)をyとする。
AM9:00から2時間、20kmを移動しているので、xy平面座標で表すと
(x,y)=(2,20)
時速を求める際、「時速=距離/時間」が成り立つので、
時速=距離/時間=y/xとなり、求めるA君の平均時速=20/2=10 10km/時間
(2)について
駅に着いたのが家を出て2時間後のAM11:00、そこから学校には12:00についているので、1時間かかったことになる。
先ほど同様にxを時間、yを距離とすると、「時速」はy/xで求められる。
代入すると、時速100km=y/1(1時間電車で移動した)より、y=100㎞
A君の移動距離を整理すると、
家から駅までが20km, 駅から学校までが100km, 合計120km
解説)
ポイントになるのは「xを時間、yを距離と置く」部分で、これによって傾きが「時速(速さ)」になっていることになります。慣れていないと「は・じ・き(小学校の算数)」の考え方のほうが早いと思うかもしれませんが、入試問題では今回出題した問題をさらに変化させてくることがあります。例えば「A君と同じ家に住むB君が1時間後に車でA君を追いかけて家を出ました、A君が駅に着くまでに追いつくには時速何キロ以上で走行する必要がありますか?」などは、1次関数の傾きと交点を利用して解くのが最適です。(答えは「20km/時間」以上です)このほかにも、普通の文章から関数に置き換える問題が様々出題されますので、「どうやったら関数に置き換えられるか?」を常に考えながら練習を繰り返してください。
解けないとヤバい確率・統計の問題と解説
最後は確率の分野からの問題です。確率は実はパターンが決まっていて、「コイン」「じゃんけん」「玉」「さいころ」「人」の主にこの5パターンです。今回は、他のパターンにも応用が利く「玉」の問題を持ってきました。
問題『確率』に関する問題
赤玉3個,白玉2個,青玉1個が入っている袋があります。
袋の中から1個取り出して色を調べ,それを袋にもどしてから,また,玉を1個取り出すとき,2個とも違う色になる確率を求めなさい
解答解説
解答)
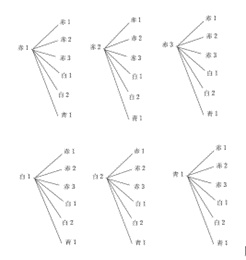
1個取り出して色を調べ,それを袋にもどす樹形図は以下の通り。
この樹形図から、全部で36通りの引き方があるとわかる。
その確率は14/36
求めたい確率は「異なる色を引く確率」なので、(1― 同じ色)=違う色の確率より、
1 ―14/36 =22/36=11/18
求める確率は11/18
解説)
高校受験数学の確率の王道の解き方は「樹形図」を漏れがないように書く方法です。実際に、とある入試問題の総評コメントでも、「すべての通りを整理して書けるかを問う問題」という見解もあったように、落ち着いて樹形図を書く力が必要になります。入試本番でケアレスミスをするとかなりもったいない分野なので、簡単そうな問題でも日ごろから樹形図として書き出す癖をつけてください。
以上が、高校受験本番で出てきた際には「解けないとヤバい」レベルの問題になります。問題を正解できるかが重要ではなく、解答解説の流れを意識して解けているかが大事なポイントですので、何度も繰り返し解いて整理してみてください。
高校受験数学問題へのアプローチ方法をプロの講師が解説!
ここからは高校受験合格に向けて、入試本番の数学の問題にどう向き合っていけばよいか、プロの塾講師目線で役立つ情報を簡単にまとめました。
高校受験数学の入試問題が解けるようになるには?【アドバイス】
受験本番レベルの問題に対応するには、1つの問題に対して複数の公式や考え方扱えるようになる必要があります。
具体的な勉強方法としては「公式単品で使えるようにする」→「入試本番の問題形式に慣れる」が手堅いステップです。数学が苦手な学生さんは、この第一段階の「公式単品で使えるようにする」で勉強が止まっていることが多々あり、入試問題のような「どの公式と考え方の組み合わせが必要か?」という解法を選び取り組み合わせる練習が不足しています。これを補うためには、今回ご紹介したような4問のような問題を「どうやって解いているか?」に注目しながら勉強していくのがオススメです。
高校入試数学で高得点を取るには?
受験生の中には、数学で高得点を目指している方もいらっしゃるかと思います。
こうした学生さんにオススメな勉強法としては、難しい問題演習を数こなすことももちろんですが、「別解を作る」という方法を常に考えて欲しいと思います。上記でご紹介した4問は、すべて別解でも解けるつくりになっています。数学の入試問題を解いて、正解して終わりではなく、日ごろから別の方法を探すことでかなり理解が深まることになり、それが結果として高得点が取れる実力につながります。
高校受験で合格するには数学は避けられない
特殊な私立高校の入試は例外として、現在の日本全国の公立高校受験においては、国数英は主要3科目で避けては通れません。どんなに数学が苦手な学生さんでも、得点につながりやすい分野から順に丁寧に対策しなければ、残念な結果になる可能性が高くなります。また、将来的な話をすると、高校数学ではかなり範囲の中学数学の知識を前提に話が進むため、ここで手を抜いていると最終的には大学入試で大変なことになります。
高校受験で数学の入試問題が解けるようになるための問題集
最後に実際に受験勉強を進めていくうえで、「どんな教材を使うべきかわからない」という学生さんのために、入試問題が解けるようになるための参考書をご紹介します。
基本的には受験する入試(高校)の過去問がベスト
まずは絶対に外せない教材が受験する入試(私立なら高校)の過去問です。これは全く同じ問題や、類題を期待して解くのではなく、「問題の質として最も信用できる」ことが理由になります。どうやったら学生の実力を正確に測れるか、各科目の専門家が何人も集まって吟味して作られた問題ですので、これを勉強しないのは邪道です。前述した通り、問題に正解して満足するのではなく、解答手順や別解を考察して何度も解きなおすと確実に実力をつけることができます。
オススメの問題集
受験する入試問題の過去問だけでも大抵の場合は十分ですが、さらに上を目指したいという方は以下の参考書がオススメです。ポイントとしては、膨大な問題数と地域によって異なる問題の傾向が経験できるためマンネリ化せずに数学の問題演習ができます。
問題集の効果を最大限に発揮するために
せっかく買った問題集を単に「解き捨て」するのはもったいないです。その効果を発揮するためにお勧めの勉強手順をご紹介します。
- まずは一周してみる(最初から正解した問題は篩にかける)
- 間違いが多い分野だけ2周目解いてみる
- の作業を次に間違いの多い分野で行う
この方法だと、受験本番もし仮に特定の分野の難易度があがっても(例えば確率が難しいなど)、死角なく勉強できているため合計点を落とさず得点できるようになります。
数学の受験問題は何度も演習を重ねることで解けるようになります。今回ご紹介した
4問や、参考書などを活用してまずはアプローチの仕方から慣れていきましょう。