「高校受験の数学が苦手」

「公式が沢山ありすぎてどれから覚えたらよいかわからない」

「公式が覚えられない、、、」

など上記のような悩みを持つ学生さんの問題を解決するため、プロの塾講師が高校受験で覚えるだけで点数が上がる数学の公式を厳選してまとめました。

簡単な練習問題と、数学の公式の効率的な覚え方も併せて解説しています。

図形の基本公式【オススメ度：★★★★★（覚えるだけ！）】

高校受験の点数アップの為に最もオススメの数学公式は“図形”の公式です。

基本問題は公式に当てはめるだけで解けるものも多く、図形というイメージのつけやすい性質から数学が苦手な学生さんであっても取り組みやすい理由から一番に覚えてほしい公式たちになります。

三角形や四角形の計算公式

まずは図形の中でも比較的簡単な三角形と四角形に関連する公式です。

三平方の定理

c²=a²+b² （直角三角形の斜辺の二辺の二乗の和は、斜辺の二乗に等しい）

練習問題: 直角三角形の直角辺の長さがそれぞれ3cmと4cmである。斜辺の長さを求めよ。

解答: c²=a²+b²より、c²=3²+4²、c²=25、c=√25=5　答え：斜辺は5cm

 

三角錐と四角錐の体積

共通して： V= ×底面の面積×高さ               

練習問題：底面が正方形で高さが6cmの四角錐の体積を求めよ。ただし、正方形の1辺の長さは5cmとする。

解答:底面積＝５×5=25、V= ×２５×6=50　答え：50cm³

 

円や球の面積と体積の計算公式

少しだけ難しくなってきますが、ここからは“円や球”のように丸い図形を中心に公式をご紹介します。

円の面積

面積=πr²

練習問題: 半径が6cmの円の面積を求めよ。

解答: 面積=π6²=36π　答え：36πcm²

 

円の周の長さ

円周=2πr

練習問題: 半径が8cmの円の周の長さを求めよ。

解答: 面積=2×π×8=16π　答え：16πcm

 

円錐の表面積と体積

表面積： S=πr(r+l) ここで、r は底面の半径、l は斜高（円錐の頂点から底面までの垂直距離）

体積： V=πr²h ここで、r は底面の半径、h は高さ

練習問題: 半径が10cmで高さが15cmの円錐の表面積を求めよ。斜面の長さは20cmとする。

解答: 表面積=π×10(10+20)=300π　答え：300πcm²

体積= V=π10²×15　答え：500πcm³

 

球の表面積

表面積=4πr²

練習問題: 半径が5cmの球の表面積を求めよ。

解答: 表面積=4π5²=100π　答え：100πcm²

 

球の体積

体積=πr³

練習問題: 半径が3cmの球の体積を求めよ。

解答: 体積=π3³=36π　答え：36πcm³

 

【ちょっと応用】扇形の計算公式

ここからは少し応用的な図形の公式になります。ちょっと難しいですが、難しくなる分問題のパターンは他の図形よりもかなり少なくなってきます。問題を沢山解いて、ひとまず答えだけでも出せるようにしておくと点数アップに直結します。

扇形の面積

面積=r²θ （ただし、θ は弧度法での中心角）

練習問題: 半径が6cmで中心角が60度の扇形の面積を求めよ。

解答: 面積=6²θ=18θ、ここでθ=×60=面積＝18×＝6π　答え：6πcm²

 

弧の長さ

弧の長さ=rθ （ただし、θ は弧度法での中心角）

練習問題: 半径が8cmで中心角が45度の扇形の弧の長さを求めよ。

解答: 面積=8θ=8θ、ここでθ=×45=弧の長さ＝8×＝2π　答え：2πcm

 

【ちょっと応用】合同条件と相似条件の基本公式

図形の中で一番「理屈っぽい」のがこの合同と相似条件の範囲です。この公式（条件）は覚えてないとそもそも問題が解けないですが、覚えたからといって得点できるわけでもありません。

「どうしてその条件が根拠になるのか？」理解しながら問題をといていく必要があります。今回は、ひとまず公式として覚えることがメインなので、かなり簡単な練習問題をつけています。

三角形の合同条件の基本

３組の辺がそれぞれ等しい。

２組の辺とその間の角がそれぞれ等しい。

１組の辺とその両端の角がそれぞれ等しい。

練習問題: 二つの三角形があり、それぞれの角度が次の通りです。三角形PQRの角度は∠P=60°、∠Q=40°、∠R=80°、三角形XYZの角度は∠X=60°、∠Y=80°、∠Z=40°である。この三角形は合同といえるか？また、合同である場合その条件を記せ。

解答：合同である、２組の辺とその間の角がそれぞれ等しい。

 

直角三角形の合同条件

直角三角形の斜辺と１つの鋭角がそれぞれ等しい。

直角三角形の斜辺と他の１辺がそれぞれ等しい。

練習問題: 二つの直角三角形があります。それぞれの三角形の一辺の長さが次のように与えられています。 三角形ABCの辺の長さはAB=3cm、BC=4cm、CA=5cmであり、三角形DEFの辺の長さはDE=5cm、EF=12cm、FD=13cmです。この直角三角形は合同といえるか？また、合同である場合その条件を記せ。

解答：合同である、直角三角形の斜辺と他の１辺がそれぞれ等しい。

 

 

三角形の相似条件の基本

３組の辺の比がすべて等しい。

２組の辺の比とその間の角がそれぞれ等しい。

２組の角がそれぞれ等しい。

練習問題: 二つの三角形があります。それぞれの三角形の各辺の長さが次のように与えられています。 三角形ABCの辺の長さはAB=6cm、BC=8cm、CA=10cmであり、三角形DEFの辺の長さはDE=9cm、EF=12cm、FD=15cmです。この三角形は相似といえるか？また、相似である場合その条件を記せ。

解答：相似である、３組の辺の比がすべて等しい。

 

計算系の基本公式【オススメ度：★★★（最低限知っててほしい）】

図形の次に抑えてほしいのが、今回ご紹介する基本計算の公式です。

図形の公式のように「覚えたら解ける」といったものではありませんが、今回ご紹介する以下の4つは少なくとも覚えていないと、ほとんどの高校受験数学の問題が解けなくなります。

簡単な問題を解きながらゆっくり使い方を整理していきましょう。

基本計算公式

基本計算のパートでは「有利化」「展開公式」「因数分解」3つを覚えてもらいます。

いろんな問題にも挑戦して欲しいですが、数学が苦手な方は今回載せている問題を覚えてしまうくらい何回も解くことで使い方がつかめてくると思います。

ルートの有利化

a/√b＝(√b)/√b＝(a√b)/b

練習問題: １/√２を有利化せよ。

解答：　1/√2＝√2/√2＝√2/2　答え：　√2/2

 

乗法公式（展開公式）

(x + a)(x + b) = x² +(a + b)x + ab

(x + a)² = x² + 2ax + a²

(x + a)(x – a)= x² – a²

練習問題:次の式を展開せよ。

(x + 2)(x + 3)

(x + 3)²

(x + 3)(x – 3)

 

解答：(x + 2)(x + 3) = x² +(2 + 3)x + 2×3= x² +5x + 6

(x + 3)²= x² + 2×3x + 3²= x² + 6x + 9

(x + 3)(x – 3)= x² – 3²= x² – 9

 

因数分解

a² – b² = (a+b)(a-b)

a² + 2ab +b² = (a+b)²

x² + (a+b)x + ab = (x+a)(x+b)

練習問題:次の式を因数分解せよ。

x² +5x + 6

x² + 6x + 9

x² – 9

 

解答：

x² +(2 + 3)x + 2×3= (x + 2)(x + 3)

x² + 2×3x + 3²= (x + 3)²

x² – 3²= (x + 3)(x – 3)

 

二次方程式と解の公式

「解の公式」は因数分解ができない二次方程式の解（X）を求める際に使います。

ですので、実際に問題を解く際は「因数分解してみる→因数分解ができない→解の公式をつかう」のステップで使うようにしてください。（時々なんでも解の公式でやっちゃおうとする学生さんがいますがNGです。）

解の公式

ax²+bx+c=0の時、x=(-b±√(b^2-4ac))/2a

練習問題:次の式の解を求めよ。

x²-5x+6=0

解答：x=(-（-5）±√((-5)^2-4×1×6))/(2×1)= (５±√(25-24))/2 =3,2

 

 

 

関数とグラフの基本公式【オススメ度：★★（応用した問題が頻出）】

続いては、関数の式とグラフの形を公式のように覚えていきましょう。

中学数学での関数の知識は、高校数学でも「必ず」必要な知識になってくるので、苦手意識がある方でも最終的にはこれからご紹介することだけでも覚えておいてください。

高校入試アップに直結するかといわれると難しい単元ですが、将来的に重要な知識であることは間違いありません。

関数の種類と形

関数を勉強するうえでは「式の形」と「グラフの形」の両方をセットで覚えることが重要です。

比例（復習）

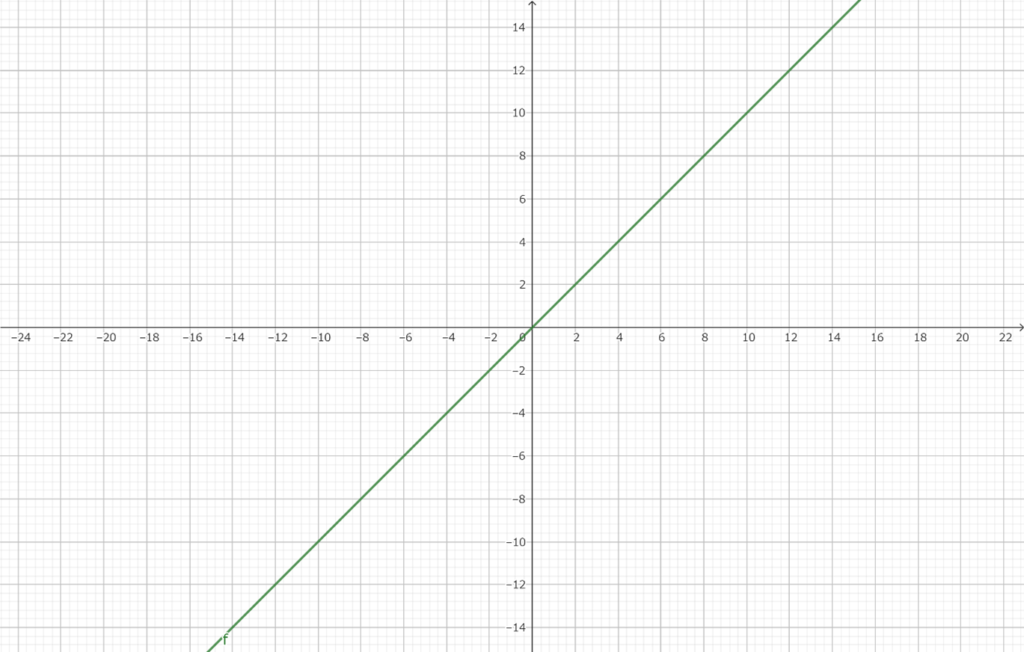
y=ax

練習問題:y=2,4,6,8となる関数を式で表せ。

解答：y=2x

 

反比例

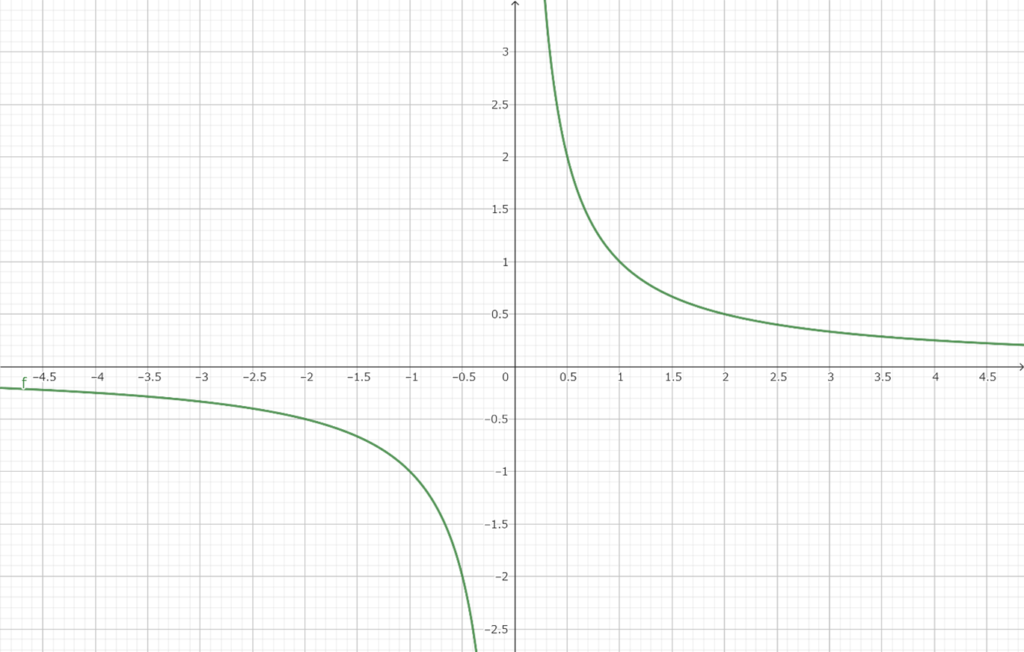
y=Ｘ/a

練習問題:y=30,27,24,21となる関数を式で表せ。

解答：y=Ｘ/3

 

一次関数

y=ax＋b

練習問題：点s（0.4）と点t(2,8)を通る直線の式を求めよ。

解答：それぞれの点を公式に代入すると、

4=b、8=a×2+ｂ、b＝４を代入数ｒとa=2より　答え：y=2x+4

 

二次関数

y=ax²

練習問題：二次関数 ｙ＝ax²が(3,18) を通る。係数aを求めよ

解答：(3,18) を代入すると、

18=a×3²より　答え：a=2

 

高校受験数学の公式を覚えるオススメの方法【勉強法】

ここからは、高校受験の数学の公式の効率的な覚え方をわかりやすくご紹介していきます。

数学の公式を覚えるテクニックだけでなく、公式を覚えるのにオススメの参考書も併せてご紹介するので、教材選びに役立ててください。

数学の公式は問題を解きながら覚えるのが最短！

早速結論から、数学の公式は「問題を解きながら覚えるのが一番効率的」です。

例えば皆さんはゲームをするとき、いちいち取扱説明書でコマンドを暗記してからゲームをやりますか？違いますね。

それと同じです。

実際に数学の問題を解きながら（プレイしながら）数学の公式の使い方を覚えるのが自然で無理のない方法なんです。

コツは「覚えるまで同じ問題を何回も解く」ことです。

復習は「その日・次の日・一週間」の3stepで！

もう一つテクニックがあります。

それは復習のタイミングを「その日・次の日・一週間」の3stepで行うことです。

これは科学的に人間が忘れるタイミングをうまく狙った復習テクニックで、数学の勉強以外のすべての勉強にも生かせる最強の復習サイクルになります。

高校受験の数学公式をマスターするためにオススメの参考書

最後に高校受験の数学公式をマスターするためにオススメの参考書を1つだけご紹介します。

「数学の公式を覚えるためにどんな問題を解いたらいいかわからない」といった方はまずはこの参考書を何度も解いてみてください。

 

参考書：高校入試 でる順ターゲット 中学数学公式・解法100 四訂版

 

オススメポイントとしては、公式とその練習問題が豊富な点です。 

しっかり数学の公式を覚えて一点でも多く得点していきましょう！

同じカテゴリーの記事